Touch-screen filtering
23 Jan 2015
Although the tslib library is often used on embedded Linux systems for touch-screen filtering, it can be done in a flexible and effective way in just a hundred or so lines of C++. The method described here has been tested on both a resistive touch-screen and a capacitative touch-pad.
A single-touch device gives us a continuous stream of samples. Each sample contains ADC readings for X, Y and pressure (for capacitative devices – resistive devices will give a boolean pressure value). The X and Y ADC readings relate in some way to the physical location of the pressure applied to the screen, but you can’t use them directly. There are several problems that you need to overcome first:
They are uncalibrated – you don’t know the ratio of ADC units to screen pixels, or what values correspond to the screen extents.
The X and Y channels may be swapped (this is surprisingly often the case).
The ADC values are overlaid with a continuous stream of low-amplitude noise.
Often, noise causes ADC conversions to spike wildly in one direction.
Light brushes on a resistive touch screen, where the two membranes don’t make good contact, give inaccurate positional readings.
The filtering scheme described here solves all of these problems. The overall structure of the filter is shown in the following diagram:
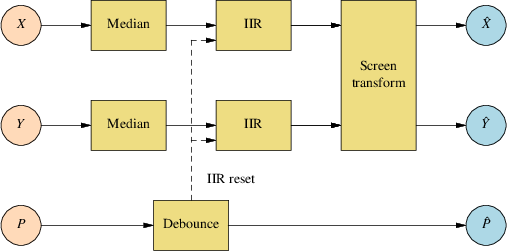
The sample filtering and screen transforms will be described separately.
Sample filtering
By “sample filtering”, we mean the process of taking raw X, Y and pressure readings and processing them into something less noisy and more reliable. The end result will still be uncalibrated (and possibly channel-swapped). We will use the following data structures in the descriptions below:
struct point {
int x, y;
point() { }
point(int _x, int _y) : x(_x), y(_y) { }
};
struct sample {
point l;
bool p;
sample() { }
sample(const point& _l, bool _p) : l(_l), p(_p) { }
};We’ll assume that you have a function to read raw samples from the
touch-sensor device, which returns them in the form of a
sample structure.
Note that if you want to track degrees of pressure on a capacitative
device, you’ll need to replace the pressure value with an
int, rather than a bool, and substitute where
appropriate in the following code.
Median filter
The purpose of median filtering is to remove the transient spikes that occur in some ADC conversions. The way we do this is by keeping a rolling buffer of the last 5 raw samples, and at each step, picking the median of the 5 as output. Since the array size is known in advance and fixed, the median selection can be done using an optimal sorting network:
class median_filter {
public:
median_filter()
{
s.fill(0);
}
int operator()(int x)
{
s[0] = s[1];
s[1] = s[2];
s[2] = s[3];
s[3] = s[4];
s[4] = x;
std::array<int, 5> t = s;
cmp_swap(t[0], t[1]);
cmp_swap(t[2], t[3]);
cmp_swap(t[0], t[2]);
cmp_swap(t[1], t[4]);
cmp_swap(t[0], t[1]);
cmp_swap(t[2], t[3]);
cmp_swap(t[1], t[2]);
cmp_swap(t[3], t[4]);
cmp_swap(t[2], t[3]);
return t[2];
}
private:
static inline void cmp_swap(int& a, int& b)
{
if (a > b)
std::swap(a, b);
}
std::array<int, 5> s;
};IIR filter
The IIR filter is the next step in the chain for each position channel. After removing the worst spikes, we then smooth to remove low-level noise using an infinite impulse response filter. There is a trade-off between noise removal and responsiveness, so the filter is parameterized:
template<int N, int D>
class iir_filter {
public:
iir_filter() : s(0) { }
int operator()(int x, bool reset = false)
{
if (reset) {
s = x;
return x;
}
s = (N * s + (D - N) * x + D / 2) / D;
return s;
}
private:
int s;
};The parameters N and D specify the level of
smoothing in the form of a fraction (N/D). Note also the
reset parameter to the filter. This is used to reset the
filter state when the first valid touch is received, so that the noise
received before the touch has no effect.
The median filter and IIR filter together form the channel filter, which we use for each of the positional ADC channels:
template<int N, int D>
class channel_filter {
public:
int operator()(int x, bool reset = false)
{
return i(m(x), reset);
}
private:
median_filter m;
iir_filter<N, D> i;
};Debounce
Touch-screens generally don’t suffer from bounce in the way that mechanical switches do, but we have a different problem that can be solved in a similar way. A light or accidental brush on the screen produces a short series of unreliable samples. In the case of a light press, the pressure sense might rapidly toggle off and on.
We filter the pressure signal by treating the pressure sensor as off until we’ve received a certain number of samples where the signal is on. When the pressure sensor turns off, we recognise it immediately:
template<int P>
class debounce_filter {
public:
debounce_filter() : s(0) { }
bool on() const
{
return s >= P;
}
bool operator()(bool x)
{
if (!x) {
s = 0;
return false;
}
if (s < P)
s++;
return on();
}
private:
int s;
};The other reason for using this filter is that the delay gives us time to fill the median filter with valid data before it’s used (assuming we set P >= 5).
Sample filtering
Combining all filters together, we get the unified sample filter:
template<int N, int D, int P>
class sample_filter {
public:
sample operator()(const sample& s)
{
const bool rst = !p.on();
return sample(point(x(s.l.x, rst), y(s.l.y, rst)), p(s.p));
}
private:
debounce_filter<P> p;
channel_filter<N, D> x;
channel_filter<N, D> y;
};
typedef sample_filter<7, 10, 5> default_sample_filter;Note the use of the debounced pressure signal to reset the state of the IIR filter.
Screen transform and calibration
Having filtered the touch-screen samples, you need to figure out what screen positions they represent. As stated above, there may be arbitrary scaling and shifting of both axes (including negative scales), and possible channel swapping.
Fortunately, there’s a simple method of calibration, requiring only three test touches to obtain all the necessary information:
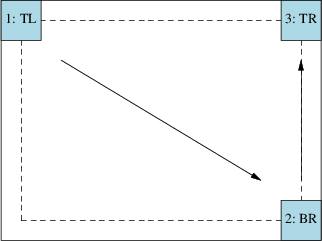
From the first two touch locations (TL and BR), we determine the range of the ADC readings on both channels, minus some margin. In other words, we have the ADC readings that correspond to the top-left and bottom-right corners of the dashed box.
The third touch (TR) tells us whether the X and Y channels are
swapped, and also acts as a cross-validation of the calibration data. We
check to see if the third touch is within the box we expect it to be. If
not, we try swapping channels and testing again. This is shown below in
the calibrate method, which returns true for successful
calibration:
class screen_transform {
public:
screen_transform() :
adc_min(0, 0),
adc_range(0, 0),
dim(0, 0),
margin(0),
swap_coords(false) { }
bool calibrate(const point& tl, const point& br, const point& tr,
int m, const point& d)
{
screen_transform next;
next.adc_min = tl;
next.adc_range = point(br.x - tl.x, br.y - tl.y);
next.dim = d;
next.margin = m;
next.swap_coords = false;
point t = next(tr);
if ((t.x >= d.x - m * 2) && (t.y < m * 2)) {
*this = next;
return true;
}
next.swap_coords = true;
t = next(tr);
if ((t.x >= d.x - m * 2) && (t.y < m * 2)) {
*this = next;
return true;
}
return false;
}
point operator()(const point& p) const
{
if (swap_coords)
return point(ch_scale(adc_min.y, adc_range.y, dim.x, p.y),
ch_scale(adc_min.x, adc_range.x, dim.y, p.x));
return point(ch_scale(adc_min.x, adc_range.x, dim.x, p.x),
ch_scale(adc_min.y, adc_range.y, dim.y, p.y));
}
private:
int ch_scale(int adc_min, int adc_range, int dim, int x) const
{
if (adc_range)
x = ((x - adc_min) * (dim - margin * 2) +
(adc_range / 2)) / adc_range + margin;
if (x < 0)
return 0;
if (x >= dim)
return dim - 1;
return x;
}
point adc_min;
point adc_range;
point dim;
int margin;
bool swap_coords;
};